Bleiben wir in dieser und den kommenden Wochen noch bei feenschach-Retrobeispielen aus der Zeit der Jahrtausendwende.
feenschach ist dafür bekannt, dass dort auch orthodoxe, aber unkonventionelle Aufgaben gut erscheinen können — „nur“ Märchenschach ist dort trotz des Namens gar nicht erforderlich.
Hier stellt uns Michel Caillaud eine Aufgabe mit sehr ungewöhnlicher Zwillingsbildung vor: Üblich ist ja, entweder mehr als eine Lösung für die gleiche Stellung ohne Änderungen zu fordern, und der Unterschied liegt dann meist schon im ersten Zug — oder halt eine Stellungsänderung.

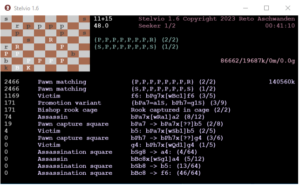
Michel Caillaud
feenschach 2000
Beweispartie in 15 Zügen, zwei Varianten im 5. weißen Zug (14+14)
In dieser Aufgabe haben wir nun den Fall, dass die ersten vier Züge völlig identisch sind, dann quasi zwei Varianten entstehen. In einer Notation, die sich hauptsächlich für Hilfsmatts, aber auch allgemein fürs Hilfsspiel durchgesetzt hat, würde man notieren: 1.1;1.1;1.1;1.1;2.1;1…
Damit wird für jede „Zählstelle“ der einzelnen Züge angegeben, wie viele verschiedene vorgesehen sind: Hier sind es im 5. weißen Zug zwei mögliche, und danach geht es dann eindeutig weiter, das Spiel verzweigt sich dort also.
Interessant wird dann zu beobachten sein, wie sich die beiden Varianten zueinander verhalten, ob es inhaltliche oder formale Gemeinsamkeiten, aber auch Unterschiede gibt. Bei Beweispartie-Mehrlingen lässt es sich ja generell nicht vermeiden, dass eine Menge Züge in den Varianten gleich sind. Hier ist das etwa für den Weg des schwarzen Königs und auch des weißen Springers zu erwarten.
Weiterlesen →