Heute möchte ich euch eine Alice-Schach Beweispartie aus René J. Millours neuem Buch „Subtleties on 64 Squares“ vorstellen.
Kennt ihr Alice-Schach? Wenn nicht, hier die Definition aus dem immer wieder empfehlenswerten Schwalbe-Lexikon:
„Es wird auf zwei 8×8-Brettern gespielt: Bretter A und B. Nach jedem Zug (wahlweise auf einem der beiden Bretter) wird der gezogene Stein als unmittelbare Zugfolge auf das analoge leere Feld des anderen Brettes versetzt. Ist das zugehörige Feld nicht leer, wäre der entsprechende Zug illegal. Ein Schlagfall ist also nur auf demjenigen Brett möglich, auf dem der Zug auch startete. Geschlagene Steine verschwinden vom Brett. Der König darf durch einen Zug seiner Partei weder vor dem Brettwechsel des Zugsteines noch danach einem Schachgebot auf seinem Brett im herkömmlichen Sinne ausgesetzt sein. In der Partieanfangsstellung stehen alle 32 Steine auf Brett A.“
Es hat sich eingebürgert, die Alice-Stellungen auf nur einem Brett darzustellen und dabei die Klötze, die auf Brett B stehen, auf den Kopf zu stellen: Laut Definition kann ja nie das gleiche Feld auf Brett A und Brett B besetzt sein.
Interessante Möglichkeiten gibt es mit Alice-Schach: Zum Warmwerden versucht doch einmal, einen weißen und einen schwarzen Bauern auf der gleichen Linie schlagfrei aneinander vorbei zu bringen.
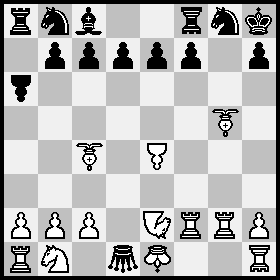
René J. Millour
StrateGems 2007, 3. Preis
Beweispartie in 21,0 Zügen, Alice-Schach A(8+11) B(6+3)
Auch wenn das im ersten Moment kompliziert ausschaut, so kann man gerade bei Alice-Schach sehr gut Züge zählen: Man sieht sofort, ob ein Stein eine gerade (aufrecht stehend) oder ungerade (auf dem Kopf stehend) Anzahl von Zügen gemacht hat. Übrigens verschwinden bei der Rochade König UND Turm auf Brett B.
Beim Züge-Zählen habe ich mich an René’s Beschreibung im Buch orientiert.
Weiterlesen →
